反向傳播的目的是計(jì)算成本函數(shù)C對(duì)網(wǎng)絡(luò)中任意w或b的偏導(dǎo)數(shù)。一旦我們有了這些偏導(dǎo)數(shù)，我們將通過(guò)一些常數(shù) α的乘積和該數(shù)量相對(duì)于成本函數(shù)的偏導(dǎo)數(shù)來(lái)更新網(wǎng)絡(luò)中的權(quán)重和偏差。這是流行的梯度下降算法。而偏導(dǎo)數(shù)給出了最大上升的方向。因此，關(guān)于反向傳播算法，我們繼續(xù)查看下文。

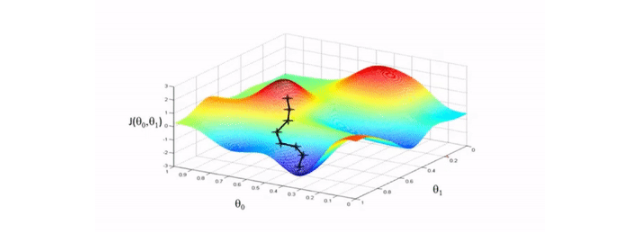
我們向相反的方向邁出了一小步——最大下降的方向，也就是將我們帶到成本函數(shù)的局部最小值的方向。

圖示演示:

反向傳播算法中Sigmoid函數(shù)代碼演示：

# 實(shí)現(xiàn) sigmoid 函數(shù)return 1 / (1 + np.exp(-x))def sigmoid_derivative(x):# sigmoid 導(dǎo)數(shù)的計(jì)算return sigmoid(x)*(1-sigmoid(x))

反向傳播算法中ReLU 函數(shù)導(dǎo)數(shù)函數(shù)代碼演示：

def relu_derivative(x): # ReLU 函數(shù)的導(dǎo)數(shù)d = np.array(x, copy=True) # 用于保存梯度的張量d[x < 0] = 0 # 元素為負(fù)的導(dǎo)數(shù)為 0d[x >= 0] = 1 # 元素為正的導(dǎo)數(shù)為 1return d

實(shí)例擴(kuò)展：

BP反向傳播算法Python簡(jiǎn)單實(shí)現(xiàn)

import numpy as np# 'pd' 偏導(dǎo)def sigmoid(x): return 1 / (1 + np.exp(-x))def sigmoidDerivationx(y): return y * (1 - y)if __name__ == '__main__': #初始化 bias = [0.35, 0.60] weight = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55] output_layer_weights = [0.4, 0.45, 0.5, 0.55] i1 = 0.05 i2 = 0.10 target1 = 0.01 target2 = 0.99 alpha = 0.5 #學(xué)習(xí)速率 numIter = 10000 #迭代次數(shù) for i in range(numIter): #正向傳播 neth1 = i1*weight[1-1] + i2*weight[2-1] + bias[0] neth2 = i1*weight[3-1] + i2*weight[4-1] + bias[0] outh1 = sigmoid(neth1) outh2 = sigmoid(neth2) neto1 = outh1*weight[5-1] + outh2*weight[6-1] + bias[1] neto2 = outh2*weight[7-1] + outh2*weight[8-1] + bias[1] outo1 = sigmoid(neto1) outo2 = sigmoid(neto2) print(str(i) + ', target1 : ' + str(target1-outo1) + ', target2 : ' + str(target2-outo2)) if i == numIter-1: print('lastst result : ' + str(outo1) + ' ' + str(outo2)) #反向傳播 #計(jì)算w5-w8(輸出層權(quán)重)的誤差 pdEOuto1 = - (target1 - outo1) pdOuto1Neto1 = sigmoidDerivationx(outo1) pdNeto1W5 = outh1 pdEW5 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W5 pdNeto1W6 = outh2 pdEW6 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W6 pdEOuto2 = - (target2 - outo2) pdOuto2Neto2 = sigmoidDerivationx(outo2) pdNeto1W7 = outh1 pdEW7 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W7 pdNeto1W8 = outh2 pdEW8 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W8 # 計(jì)算w1-w4(輸出層權(quán)重)的誤差 pdEOuto1 = - (target1 - outo1) #之前算過(guò) pdEOuto2 = - (target2 - outo2) #之前算過(guò) pdOuto1Neto1 = sigmoidDerivationx(outo1) #之前算過(guò) pdOuto2Neto2 = sigmoidDerivationx(outo2) #之前算過(guò) pdNeto1Outh1 = weight[5-1] pdNeto2Outh2 = weight[7-1] pdEOuth1 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh1 + pdEOuto2 * pdOuto2Neto2 * pdNeto1Outh1 pdOuth1Neth1 = sigmoidDerivationx(outh1) pdNeth1W1 = i1 pdNeth1W2 = i2 pdEW1 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W1 pdEW2 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W2 pdNeto1Outh2 = weight[6-1] pdNeto2Outh2 = weight[8-1] pdOuth2Neth2 = sigmoidDerivationx(outh2) pdNeth2W3 = i1 pdNeth2W4 = i2 pdEOuth2 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh2 + pdEOuto2 * pdOuto2Neto2 * pdNeto2Outh2 pdEW3 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W3 pdEW4 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W4 #權(quán)重更新 weight[1-1] = weight[1-1] - alpha * pdEW1 weight[2-1] = weight[2-1] - alpha * pdEW2 weight[3-1] = weight[3-1] - alpha * pdEW3 weight[4-1] = weight[4-1] - alpha * pdEW4 weight[5-1] = weight[5-1] - alpha * pdEW5 weight[6-1] = weight[6-1] - alpha * pdEW6 weight[7-1] = weight[7-1] - alpha * pdEW7 weight[8-1] = weight[8-1] - alpha * pdEW8 # print(weight[1-1]) # print(weight[2-1]) # print(weight[3-1]) # print(weight[4-1]) # print(weight[5-1]) # print(weight[6-1]) # print(weight[7-1]) # print(weight[8-1])

到此這篇關(guān)于python里反向傳播算法詳解的文章就介紹到這了,更多相關(guān)python里反向傳播算法是什么內(nèi)容請(qǐng)搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！