數(shù)據(jù)準(zhǔn)備

數(shù)據(jù)集（JetRail高鐵的乘客數(shù)量）下載.

假設(shè)要解決一個(gè)時(shí)序問題：根據(jù)過往兩年的數(shù)據(jù)（2012 年 8 月至 2014 年 8月），需要用這些數(shù)據(jù)預(yù)測(cè)接下來 7 個(gè)月的乘客數(shù)量。

import pandas as pd import numpy as np import matplotlib.pyplot as plt df = pd.read_csv(’train.csv’)df.head()df.shape

依照上面的代碼，我們獲得了 2012-2014 年兩年每個(gè)小時(shí)的乘客數(shù)量。為了解釋每種方法的不同之處，以每天為單位構(gòu)造和聚合了一個(gè)數(shù)據(jù)集。

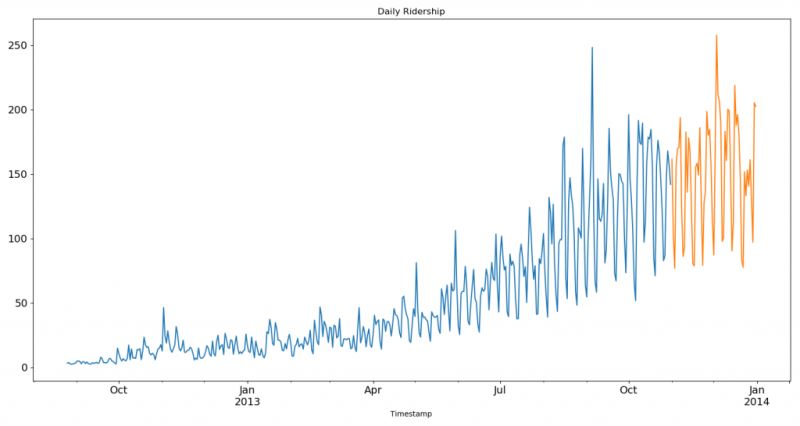
從 2012 年 8 月- 2013 年 12 月的數(shù)據(jù)中構(gòu)造一個(gè)數(shù)據(jù)集。 創(chuàng)建 train and test 文件用于建模。前 14 個(gè)月（ 2012 年 8 月- 2013 年 10 月）用作訓(xùn)練數(shù)據(jù)，后兩個(gè)月（2013 年 11 月 ? 2013 年 12 月）用作測(cè)試數(shù)據(jù)。 以每天為單位聚合數(shù)據(jù)集。

import pandas as pdimport matplotlib.pyplot as plt # Subsetting the dataset# Index 11856 marks the end of year 2013df = pd.read_csv(’train.csv’, nrows=11856) # Creating train and test set# Index 10392 marks the end of October 2013train = df[0:10392]test = df[10392:] # Aggregating the dataset at daily leveldf[’Timestamp’] = pd.to_datetime(df[’Datetime’], format=’%d-%m-%Y %H:%M’) # 4位年用Y，2位年用ydf.index = df[’Timestamp’]df = df.resample(’D’).mean() #按天采樣，計(jì)算均值 train[’Timestamp’] = pd.to_datetime(train[’Datetime’], format=’%d-%m-%Y %H:%M’)train.index = train[’Timestamp’]train = train.resample(’D’).mean() # test[’Timestamp’] = pd.to_datetime(test[’Datetime’], format=’%d-%m-%Y %H:%M’)test.index = test[’Timestamp’]test = test.resample(’D’).mean() #Plotting datatrain.Count.plot(figsize=(15,8), title= ’Daily Ridership’, fontsize=14)test.Count.plot(figsize=(15,8), title= ’Daily Ridership’, fontsize=14)plt.show()

我們將數(shù)據(jù)可視化（訓(xùn)練數(shù)據(jù)和測(cè)試數(shù)據(jù)一起），從而得知在一段時(shí)間內(nèi)數(shù)據(jù)是如何變化的。

方法1：樸素法

假設(shè) y 軸表示物品的價(jià)格，x 軸表示時(shí)間（天）

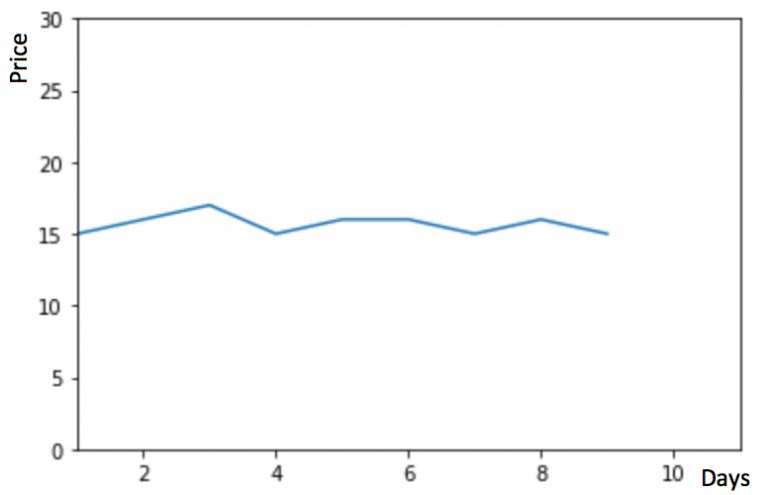
如果數(shù)據(jù)集在一段時(shí)間內(nèi)都很穩(wěn)定，我們想預(yù)測(cè)第二天的價(jià)格，可以取前面一天的價(jià)格，預(yù)測(cè)第二天的值。這種假設(shè)第一個(gè)預(yù)測(cè)點(diǎn)和上一個(gè)觀察點(diǎn)相等的預(yù)測(cè)方法就叫樸素法。即 $hat{y_{t+1}} = y_t$

dd = np.asarray(train[’Count’])y_hat = test.copy()y_hat[’naive’] = dd[len(dd) - 1]plt.figure(figsize=(12, 8))plt.plot(train.index, train[’Count’], label=’Train’)plt.plot(test.index, test[’Count’], label=’Test’)plt.plot(y_hat.index, y_hat[’naive’], label=’Naive Forecast’)plt.legend(loc=’best’)plt.title('Naive Forecast')plt.show()

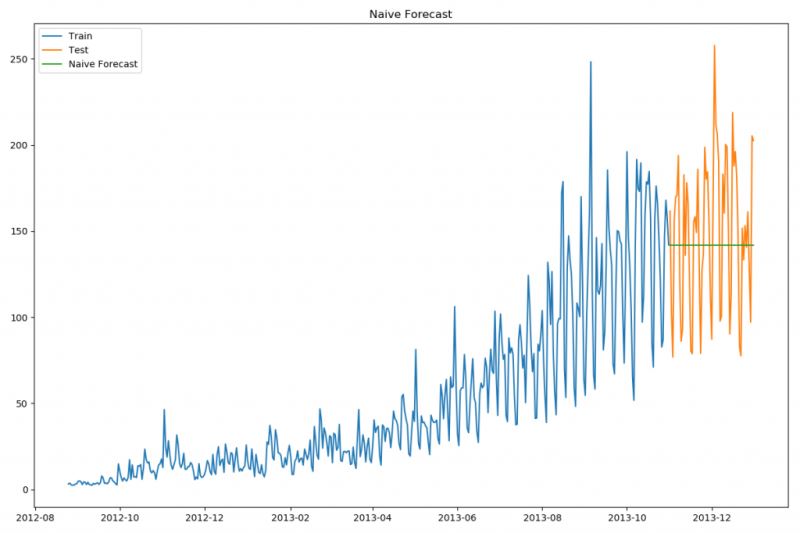
樸素法并不適合變化很大的數(shù)據(jù)集，最適合穩(wěn)定性很高的數(shù)據(jù)集。我們計(jì)算下均方根誤差，檢查模型在測(cè)試數(shù)據(jù)集上的準(zhǔn)確率：

from sklearn.metrics import mean_squared_errorfrom math import sqrt rms = sqrt(mean_squared_error(test[’Count’], y_hat[’naive’]))print(rms)

最終均方誤差RMS為：43.91640614391676

方法2：簡單平均法

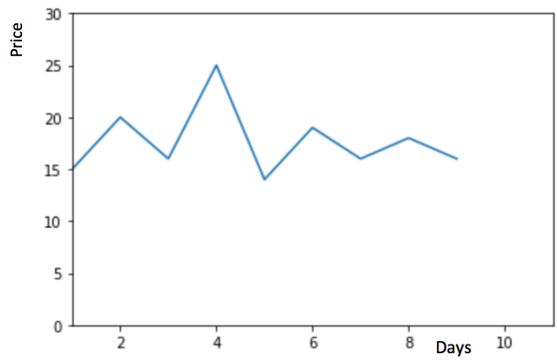
物品價(jià)格會(huì)隨機(jī)上漲和下跌，平均價(jià)格會(huì)保持一致。我們經(jīng)常會(huì)遇到一些數(shù)據(jù)集，雖然在一定時(shí)期內(nèi)出現(xiàn)小幅變動(dòng)，但每個(gè)時(shí)間段的平均值確實(shí)保持不變。這種情況下，我們可以預(yù)測(cè)出第二天的價(jià)格大致和過去天數(shù)的價(jià)格平均值一致。這種將預(yù)期值等同于之前所有觀測(cè)點(diǎn)的平均值的預(yù)測(cè)方法就叫簡單平均法。即

y_hat_avg = test.copy()y_hat_avg[’avg_forecast’] = train[’Count’].mean()plt.figure(figsize=(12,8))plt.plot(train[’Count’], label=’Train’)plt.plot(test[’Count’], label=’Test’)plt.plot(y_hat_avg[’avg_forecast’], label=’Average Forecast’)plt.legend(loc=’best’)plt.show()

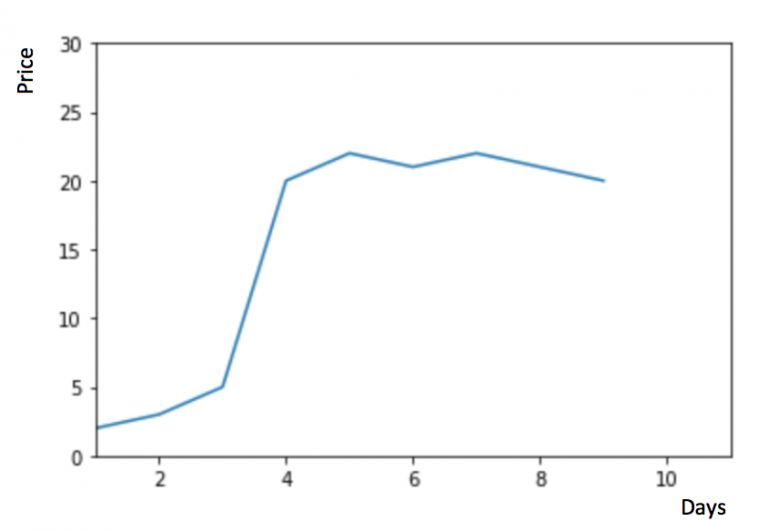
物品價(jià)格在一段時(shí)間內(nèi)大幅上漲，但后來又趨于平穩(wěn)。我們也經(jīng)常會(huì)遇到這種數(shù)據(jù)集，比如價(jià)格或銷售額某段時(shí)間大幅上升或下降。如果我們這時(shí)用之前的簡單平均法，就得使用所有先前數(shù)據(jù)的平均值，但在這里使用之前的所有數(shù)據(jù)是說不通的，因?yàn)橛瞄_始階段的價(jià)格值會(huì)大幅影響接下來日期的預(yù)測(cè)值。因此，我們只取最近幾個(gè)時(shí)期的價(jià)格平均值。很明顯這里的邏輯是只有最近的值最要緊。這種用某些窗口期計(jì)算平均值的預(yù)測(cè)方法就叫移動(dòng)平均法。

計(jì)算移動(dòng)平均值涉及到一個(gè)有時(shí)被稱為“滑動(dòng)窗口”的大小值p。使用簡單的移動(dòng)平均模型，我們可以根據(jù)之前數(shù)值的固定有限數(shù)p的平均值預(yù)測(cè)某個(gè)時(shí)序中的下一個(gè)值。這樣，對(duì)于所有的 i > p：

在上文移動(dòng)平均法可以看到，我們對(duì)“p”中的觀察值賦予了同樣的權(quán)重。但是我們可能遇到一些情況，比如“p”中每個(gè)觀察值會(huì)以不同的方式影響預(yù)測(cè)結(jié)果。將過去觀察值賦予不同權(quán)重的方法就叫做加權(quán)移動(dòng)平均法。加權(quán)移動(dòng)平均法其實(shí)還是一種移動(dòng)平均法，只是“滑動(dòng)窗口期”內(nèi)的值被賦予不同的權(quán)重，通常來講，最近時(shí)間點(diǎn)的值發(fā)揮的作用更大了。即

這種方法并非選擇一個(gè)窗口期的值，而是需要一列權(quán)重值（相加后為1）。例如，如果我們選擇[0.40, 0.25, 0.20, 0.15]作為權(quán)值，我們會(huì)為最近的4個(gè)時(shí)間點(diǎn)分別賦給40%，25%，20%和15%的權(quán)重。

方法4：簡單指數(shù)法

我們注意到簡單平均法和加權(quán)移動(dòng)平均法在選取時(shí)間點(diǎn)的思路上存在較大的差異。我們就需要在這兩種方法之間取一個(gè)折中的方法，在將所有數(shù)據(jù)考慮在內(nèi)的同時(shí)也能給數(shù)據(jù)賦予不同非權(quán)重。例如，相比更早時(shí)期內(nèi)的觀測(cè)值，它會(huì)給近期的觀測(cè)值賦予更大的權(quán)重。按照這種原則工作的方法就叫做簡單指數(shù)平滑法。它通過加權(quán)平均值計(jì)算出預(yù)測(cè)值，其中權(quán)重隨著觀測(cè)值從早期到晚期的變化呈指數(shù)級(jí)下降，最小的權(quán)重和最早的觀測(cè)值相關(guān)：

其中0≤α≤1是平滑參數(shù)。對(duì)時(shí)間點(diǎn)T+1的單步預(yù)測(cè)值是時(shí)序$y_1,…,y_T$的所有觀測(cè)值的加權(quán)平均數(shù)。權(quán)重下降的速率由參數(shù)α控制，預(yù)測(cè)值$hat{y}_x$是$alpha cdot y_t $與$(1-alpha) cdot hat{y}_x$的和。

因此，它可以寫為：

所以本質(zhì)上，我們是用兩個(gè)權(quán)重α和1−α得到一個(gè)加權(quán)移動(dòng)平均值，讓表達(dá)式呈遞進(jìn)形式。

from statsmodels.tsa.api import SimpleExpSmoothing y_hat_avg = test.copy()fit = SimpleExpSmoothing(np.asarray(train[’Count’])).fit(smoothing_level=0.6, optimized=False)y_hat_avg[’SES’] = fit.forecast(len(test))plt.figure(figsize=(16, 8))plt.plot(train[’Count’], label=’Train’)plt.plot(test[’Count’], label=’Test’)plt.plot(y_hat_avg[’SES’], label=’SES’)plt.legend(loc=’best’)plt.show()

模型中使用的α值為0.6，我們可以用測(cè)試集繼續(xù)調(diào)整參數(shù)以生成一個(gè)更好的模型。

方法5：霍爾特(Holt)線性趨勢(shì)法

假設(shè)y軸表示某個(gè)物品的價(jià)格，x軸表示時(shí)間（天）。

如果物品的價(jià)格是不斷上漲的（見上圖），我們上面的方法并沒有考慮這種趨勢(shì)，即我們?cè)谝欢螘r(shí)間內(nèi)觀察到的價(jià)格的總體模式。

每個(gè)時(shí)序數(shù)據(jù)集可以分解為相應(yīng)的幾個(gè)部分：趨勢(shì)（Trend），季節(jié)性(Seasonal)和殘差(Residual)。任何呈現(xiàn)某種趨勢(shì)的數(shù)據(jù)集都可以用霍爾特線性趨勢(shì)法用于預(yù)測(cè)。

import statsmodels.api as sm sm.tsa.seasonal_decompose(train[’Count’]).plot()result = sm.tsa.stattools.adfuller(train[’Count’])plt.show()

我們從圖中可以看出，該數(shù)據(jù)集呈上升趨勢(shì)。因此我們可以用霍爾特線性趨勢(shì)法預(yù)測(cè)未來價(jià)格。該算法包含三個(gè)方程：一個(gè)水平方程，一個(gè)趨勢(shì)方程，一個(gè)方程將二者相加以得到預(yù)測(cè)值$hat{y}$：

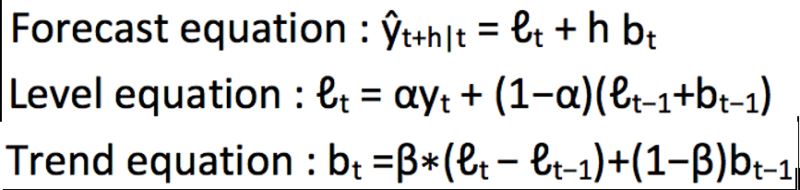
我們?cè)谏厦嫠惴ㄖ蓄A(yù)測(cè)的值稱為水平（level）。正如簡單指數(shù)平滑一樣，這里的水平方程顯示它是觀測(cè)值和樣本內(nèi)單步預(yù)測(cè)值的加權(quán)平均數(shù)，趨勢(shì)方程顯示它是根據(jù) ℓ(t)−ℓ(t−1) 和之前的預(yù)測(cè)趨勢(shì) b(t−1) 在時(shí)間t處的預(yù)測(cè)趨勢(shì)的加權(quán)平均值。

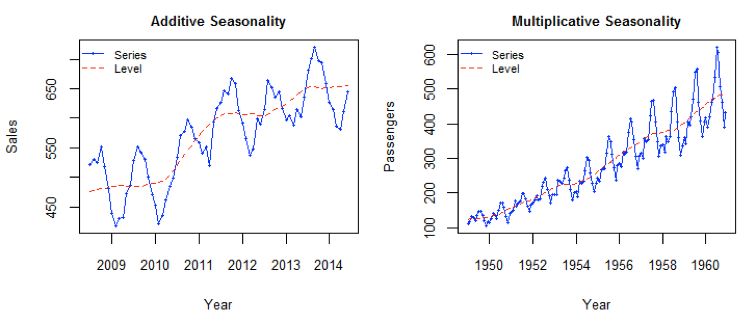
我們將這兩個(gè)方程相加，得出一個(gè)預(yù)測(cè)函數(shù)。我們也可以將兩者相乘而不是相加得到一個(gè)乘法預(yù)測(cè)方程。當(dāng)趨勢(shì)呈線性增加和下降時(shí)，我們用相加得到的方程；當(dāng)趨勢(shì)呈指數(shù)級(jí)增加或下降時(shí)，我們用相乘得到的方程。實(shí)踐操作顯示，用相乘得到的方程，預(yù)測(cè)結(jié)果會(huì)更穩(wěn)定，但用相加得到的方程，更容易理解。

from statsmodels.tsa.api import Holt y_hat_avg = test.copy() fit = Holt(np.asarray(train[’Count’])).fit(smoothing_level=0.3, smoothing_slope=0.1)y_hat_avg[’Holt_linear’] = fit.forecast(len(test)) plt.figure(figsize=(16, 8))plt.plot(train[’Count’], label=’Train’)plt.plot(test[’Count’], label=’Test’)plt.plot(y_hat_avg[’Holt_linear’], label=’Holt_linear’)plt.legend(loc=’best’)plt.show()

這種方法能夠準(zhǔn)確地顯示出趨勢(shì)，因此比前面的幾種模型效果更好。如果調(diào)整一下參數(shù)，結(jié)果會(huì)更好。

方法6：Holt-Winters季節(jié)性預(yù)測(cè)模型

在應(yīng)用這種算法前，我們先介紹一個(gè)新術(shù)語。假如有家酒店坐落在半山腰上，夏季的時(shí)候生意很好，顧客很多，但每年其余時(shí)間顧客很少。因此，每年夏季的收入會(huì)遠(yuǎn)高于其它季節(jié)，而且每年都是這樣，那么這種重復(fù)現(xiàn)象叫做“季節(jié)性”（Seasonality）。如果數(shù)據(jù)集在一定時(shí)間段內(nèi)的固定區(qū)間內(nèi)呈現(xiàn)相似的模式，那么該數(shù)據(jù)集就具有季節(jié)性。

我們之前討論的5種模型在預(yù)測(cè)時(shí)并沒有考慮到數(shù)據(jù)集的季節(jié)性，因此我們需要一種能考慮這種因素的方法。應(yīng)用到這種情況下的算法就叫做Holt-Winters季節(jié)性預(yù)測(cè)模型，它是一種三次指數(shù)平滑預(yù)測(cè)，其背后的理念就是除了水平和趨勢(shì)外，還將指數(shù)平滑應(yīng)用到季節(jié)分量上。

Holt-Winters季節(jié)性預(yù)測(cè)模型由預(yù)測(cè)函數(shù)和三次平滑函數(shù)——一個(gè)是水平函數(shù)ℓt，一個(gè)是趨勢(shì)函數(shù)bt，一個(gè)是季節(jié)分量 st，以及平滑參數(shù)α,β和γ。

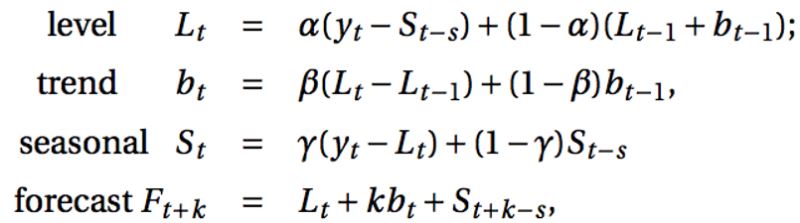
其中 s 為季節(jié)循環(huán)的長度，0≤α≤ 1, 0 ≤β≤ 1 ， 0≤γ≤ 1。水平函數(shù)為季節(jié)性調(diào)整的觀測(cè)值和時(shí)間點(diǎn)t處非季節(jié)預(yù)測(cè)之間的加權(quán)平均值。趨勢(shì)函數(shù)和霍爾特線性方法中的含義相同。季節(jié)函數(shù)為當(dāng)前季節(jié)指數(shù)和去年同一季節(jié)的季節(jié)性指數(shù)之間的加權(quán)平均值。在本算法，我們同樣可以用相加和相乘的方法。當(dāng)季節(jié)性變化大致相同時(shí)，優(yōu)先選擇相加方法，而當(dāng)季節(jié)變化的幅度與各時(shí)間段的水平成正比時(shí)，優(yōu)先選擇相乘的方法。

from statsmodels.tsa.api import ExponentialSmoothing y_hat_avg = test.copy()fit1 = ExponentialSmoothing(np.asarray(train[’Count’]), seasonal_periods=7, trend=’add’, seasonal=’add’, ).fit()y_hat_avg[’Holt_Winter’] = fit1.forecast(len(test))plt.figure(figsize=(16, 8))plt.plot(train[’Count’], label=’Train’)plt.plot(test[’Count’], label=’Test’)plt.plot(y_hat_avg[’Holt_Winter’], label=’Holt_Winter’)plt.legend(loc=’best’)plt.show()

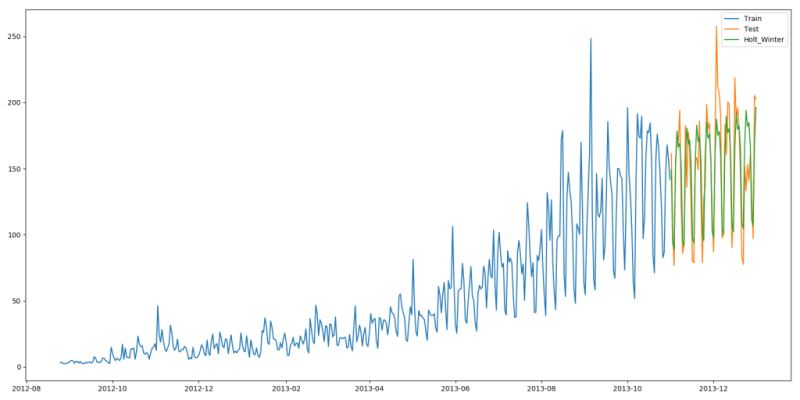
我們可以看到趨勢(shì)和季節(jié)性的預(yù)測(cè)準(zhǔn)確度都很高。我們選擇了 seasonal_period = 7作為每周重復(fù)的數(shù)據(jù)。也可以調(diào)整其它其它參數(shù)，我在搭建這個(gè)模型的時(shí)候用的是默認(rèn)參數(shù)。你可以試著調(diào)整參數(shù)來優(yōu)化模型。

方法7：自回歸移動(dòng)平均模型（ARIMA）

另一個(gè)場(chǎng)景的時(shí)序模型是自回歸移動(dòng)平均模型（ARIMA）。指數(shù)平滑模型都是基于數(shù)據(jù)中的趨勢(shì)和季節(jié)性的描述，而自回歸移動(dòng)平均模型的目標(biāo)是描述數(shù)據(jù)中彼此之間的關(guān)系。ARIMA的一個(gè)優(yōu)化版就是季節(jié)性ARIMA。它像Holt-Winters季節(jié)性預(yù)測(cè)模型一樣，也把數(shù)據(jù)集的季節(jié)性考慮在內(nèi)。

import statsmodels.api as sm y_hat_avg = test.copy()fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()y_hat_avg[’SARIMA’] = fit1.predict(start='2013-11-1', end='2013-12-31', dynamic=True)plt.figure(figsize=(16, 8))plt.plot(train[’Count’], label=’Train’)plt.plot(test[’Count’], label=’Test’)plt.plot(y_hat_avg[’SARIMA’], label=’SARIMA’)plt.legend(loc=’best’)plt.show()

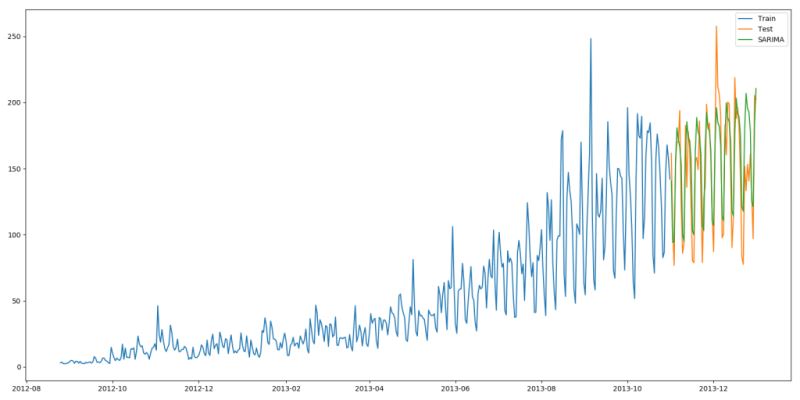
我們可以看到使用季節(jié)性 ARIMA 的效果和Holt-Winters差不多。我們根據(jù) ACF（自相關(guān)函數(shù)）和 PACF（偏自相關(guān)） 圖選擇參數(shù)。如果你為 ARIMA 模型選擇參數(shù)時(shí)遇到了困難，可以用 R 語言中的 auto.arima。

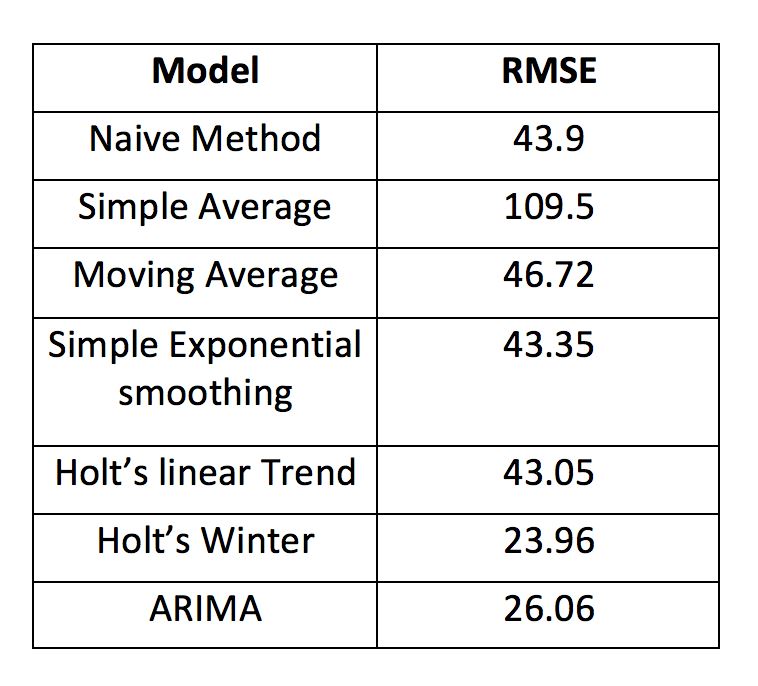
最后，我們將這幾種模型的準(zhǔn)確度比較一下：

后話

建議你在解決問題時(shí)，可以依次試試這幾種模型，看看哪個(gè)效果最好。我們從上文也知道，數(shù)據(jù)集不同，每種模型的效果都有可能優(yōu)于其它模型。因此，如果一個(gè)模型在某個(gè)數(shù)據(jù)集上效果很好，并不代表它在所有數(shù)據(jù)集上都比其它模型好。

參考鏈接：

1. 標(biāo)點(diǎn)符-用Python進(jìn)行時(shí)間序列預(yù)測(cè)的7種方法

2. 博客園-python時(shí)間序列resample參數(shù)

3. CSDN-python resample()函數(shù)（用于數(shù)據(jù)聚合）

到此這篇關(guān)于詳解用Python進(jìn)行時(shí)間序列預(yù)測(cè)的7種方法的文章就介紹到這了,更多相關(guān)Python 時(shí)間序列預(yù)測(cè)內(nèi)容請(qǐng)搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！