在過去的幾十年里，機器學(xué)習(xí)對世界產(chǎn)生了巨大的影響，而且它的普及程度似乎在不斷增長。最近，越來越多的人已經(jīng)熟悉了機器學(xué)習(xí)的子領(lǐng)域，如神經(jīng)網(wǎng)絡(luò)，這是由人類大腦啟發(fā)的網(wǎng)絡(luò)。在本文中，將介紹用于一個簡單神經(jīng)網(wǎng)絡(luò)的 Python 代碼，該神經(jīng)網(wǎng)絡(luò)對于一個 1x3 向量，分類第一個元素是否為 10。

步驟1: 導(dǎo)入 NumPy、 Scikit-learn 和 Matplotlib

import numpy as npfrom sklearn.preprocessing import MinMaxScalerimport matplotlib.pyplot as plt

我們將在這個項目中使用上述三個庫。NumPy 將用于創(chuàng)建向量和矩陣以及數(shù)學(xué)操作。Scikit-learn 將用于縮放數(shù)據(jù)，Matplotlib 將用于在神經(jīng)網(wǎng)絡(luò)訓(xùn)練期間繪圖。

步驟2: 創(chuàng)建一個訓(xùn)練和測試數(shù)據(jù)集

神經(jīng)網(wǎng)絡(luò)在大型和小型數(shù)據(jù)集的學(xué)習(xí)趨勢方面都很擅長。然而，數(shù)據(jù)科學(xué)家必須意識到過擬合的危險，這在使用小數(shù)據(jù)集的項目中更為明顯。過擬合是當(dāng)一個算法訓(xùn)練和建模過于接近一組數(shù)據(jù)點，以至于它不能很好地推廣到新的數(shù)據(jù)點。

通常情況下，過擬合的機器學(xué)習(xí)模型在訓(xùn)練的數(shù)據(jù)集上有很高的準(zhǔn)確性，但是作為一個數(shù)據(jù)科學(xué)家，目標(biāo)通常是盡可能精確地預(yù)測新的數(shù)據(jù)點。為了確保根據(jù)預(yù)測新數(shù)據(jù)點的好壞來評估模型，而不是根據(jù)對當(dāng)前數(shù)據(jù)點的建模好壞來評估模型，通常將數(shù)據(jù)集拆分為一個訓(xùn)練集和一個測試集(有時是一個驗證集)。

input_train = np.array([[0, 1, 0], [0, 1, 1], [0, 0, 0], [10, 0, 0], [10, 1, 1], [10, 0, 1]])output_train = np.array([[0], [0], [0], [1], [1], [1]])input_pred = np.array([1, 1, 0]) input_test = np.array([[1, 1, 1], [10, 0, 1], [0, 1, 10], [10, 1, 10], [0, 0, 0], [0, 1, 1]])output_test = np.array([[0], [1], [0], [1], [0], [0]])

在這個簡單的神經(jīng)網(wǎng)絡(luò)中，我們將1x3向量分類，10作為第一個元素。使用 NumPy 的 array 函數(shù)創(chuàng)建輸入和輸出訓(xùn)練集和測試集，并創(chuàng)建 input_pred 以測試稍后將定義的 prediction 函數(shù)。訓(xùn)練和測試數(shù)據(jù)由6個樣本組成，每個樣本具有3個特征，由于輸出已經(jīng)給出，我們理解這是監(jiān)督式學(xué)習(xí)的一個例子。

第三步: 擴展數(shù)據(jù)集

許多機器學(xué)習(xí)模型不能理解例如單位之間的區(qū)別，自然而然地對高度的特征應(yīng)用更多的權(quán)重。這會破壞算法預(yù)測新數(shù)據(jù)點的能力。此外，訓(xùn)練具有高強度特征的機器學(xué)習(xí)模型將會比需要的慢，至少如果使用梯度下降法。這是因為當(dāng)輸入值在大致相同的范圍內(nèi)時，梯度下降法收斂得更快。

scaler = MinMaxScaler()input_train_scaled = scaler.fit_transform(input_train)output_train_scaled = scaler.fit_transform(output_train)input_test_scaled = scaler.fit_transform(input_test)output_test_scaled = scaler.fit_transform(output_test)

在我們的訓(xùn)練和測試數(shù)據(jù)集中，這些值的范圍相對較小，因此可能沒有必要進行特征擴展。然而，這樣可以使得小伙伴們使用自己喜歡的數(shù)字，而不需要更改太多的代碼。由于 Scikit-learn 包及其 MinMaxScaler 類，在 Python 中實現(xiàn)特征伸縮非常容易。只需創(chuàng)建一個 MinMaxScaler 對象，并使用 fit_transform 函數(shù)將非縮放數(shù)據(jù)作為輸入，該函數(shù)將返回相同的縮放數(shù)據(jù)。Scikit-learn 包中還有其他縮放功能，我鼓勵您嘗試這些功能。

第四步: 創(chuàng)建一個神經(jīng)網(wǎng)絡(luò)類

要熟悉神經(jīng)網(wǎng)絡(luò)的所有元素，最簡單的方法之一就是創(chuàng)建一個神經(jīng)網(wǎng)絡(luò)類。這樣一個類應(yīng)該包括所有的變量和函數(shù)，將是必要的神經(jīng)網(wǎng)絡(luò)工作正常。

class NeuralNetwork(): def __init__(self, ): self.inputSize = 3 self.outputSize = 1 self.hiddenSize = 3 self.W1 = np.random.rand(self.inputSize, self.hiddenSize) self.W2 = np.random.rand(self.hiddenSize, self.outputSize) self.error_list = [] self.limit = 0.5 self.true_positives = 0 self.false_positives = 0 self.true_negatives = 0 self.false_negatives = 0 def forward(self, X): self.z = np.matmul(X, self.W1) self.z2 = self.sigmoid(self.z) self.z3 = np.matmul(self.z2, self.W2) o = self.sigmoid(self.z3) return o def sigmoid(self, s): return 1 / (1 + np.exp(-s)) def sigmoidPrime(self, s): return s * (1 - s) def backward(self, X, y, o): self.o_error = y - o self.o_delta = self.o_error * self.sigmoidPrime(o) self.z2_error = np.matmul(self.o_delta, np.matrix.transpose(self.W2)) self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2) self.W1 += np.matmul(np.matrix.transpose(X), self.z2_delta) self.W2 += np.matmul(np.matrix.transpose(self.z2), self.o_delta) def train(self, X, y, epochs): for epoch in range(epochs): o = self.forward(X) self.backward(X, y, o) self.error_list.append(np.abs(self.o_error).mean()) def predict(self, x_predicted): return self.forward(x_predicted).item() def view_error_development(self): plt.plot(range(len(self.error_list)), self.error_list) plt.title(’Mean Sum Squared Loss’) plt.xlabel(’Epoch’) plt.ylabel(’Loss’) def test_evaluation(self, input_test, output_test): for i, test_element in enumerate(input_test): if self.predict(test_element) > self.limit and output_test[i] == 1: self.true_positives += 1 if self.predict(test_element) < self.limit and output_test[i] == 1: self.false_negatives += 1 if self.predict(test_element) > self.limit and output_test[i] == 0: self.false_positives += 1 if self.predict(test_element) < self.limit and output_test[i] == 0: self.true_negatives += 1 print(’True positives: ’, self.true_positives, ’nTrue negatives: ’, self.true_negatives, ’nFalse positives: ’, self.false_positives, ’nFalse negatives: ’, self.false_negatives, ’nAccuracy: ’, (self.true_positives + self.true_negatives) / (self.true_positives + self.true_negatives + self.false_positives + self.false_negatives))

步驟4.1: 創(chuàng)建一個 Initialize 函數(shù)

當(dāng)我們在 Python 中創(chuàng)建一個類以便正確地初始化變量時，會調(diào)用 __init__ 函數(shù)。

def __init__(self, ): self.inputSize = 3 self.outputSize = 1 self.hiddenSize = 3 self.W1 = torch.randn(self.inputSize, self.hiddenSize) self.W2 = torch.randn(self.hiddenSize, self.outputSize) self.error_list = [] self.limit = 0.5 self.true_positives = 0 self.false_positives = 0 self.true_negatives = 0 self.false_negatives = 0

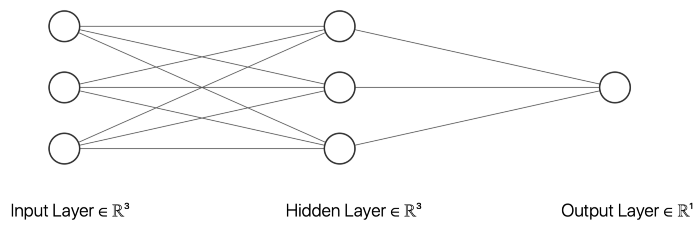
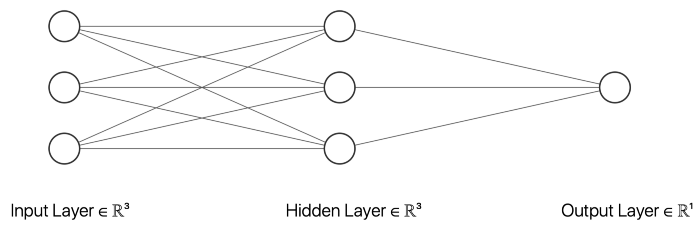
在這個例子中，我選擇了一個有三個輸入節(jié)點、三個隱藏層節(jié)點和一個輸出節(jié)點的神經(jīng)網(wǎng)絡(luò)。以上的 __init__ 函數(shù)初始化描述神經(jīng)網(wǎng)絡(luò)大小的變量。inputSize 是輸入節(jié)點的數(shù)目，它應(yīng)該等于輸入數(shù)據(jù)中特征的數(shù)目。outputSize 等于輸出節(jié)點數(shù)，hiddenSize 描述隱藏層中的節(jié)點數(shù)。此外，我們的網(wǎng)絡(luò)中不同節(jié)點之間的權(quán)重將在訓(xùn)練過程中進行調(diào)整。

除了描述神經(jīng)網(wǎng)絡(luò)的大小和權(quán)重的變量之外，我還創(chuàng)建了幾個在創(chuàng)建神經(jīng)網(wǎng)絡(luò)對象時初始化的變量，這些對象將用于評估目的。誤差列表將包含每個時期的平均絕對誤差(MAE) ，這個極限將描述一個向量應(yīng)該被分類為一個向量，元素10作為第一個元素而不是。然后，還有一些變量可以用來存儲真實陽性、假陽性、真實陰性和假陰性的數(shù)量。

步驟4.2: 創(chuàng)建一個前向傳播函數(shù)

前向傳播函數(shù)的作用是通過神經(jīng)網(wǎng)絡(luò)的不同層次進行迭代，以預(yù)測特定 epoch 的輸出。然后，根據(jù)預(yù)測輸出和實際輸出之間的差異，在反向傳播的過程中更新權(quán)重。

def forward(self, X): self.z = np.matmul(X, self.W1) self.z2 = self.sigmoid(self.z) self.z3 = np.matmul(self.z2, self.W2) o = self.sigmoid(self.z3) return o

為了計算每一層中每個節(jié)點的值，前一層中節(jié)點的值將被乘以適當(dāng)?shù)臋?quán)重，然后應(yīng)用非線性激活函數(shù)來擴大最終輸出函數(shù)的可能性。在這個例子中，我們選擇了 Sigmoid 作為激活函數(shù)，但也有許多其他的選擇。

步驟4.3: 創(chuàng)建一個反向傳播函數(shù)

反向傳播是對神經(jīng)網(wǎng)絡(luò)中不同節(jié)點的權(quán)值進行更新，從而決定其重要性的過程。

def backward(self, X, y, o): self.o_error = y - o self.o_delta = self.o_error * self.sigmoidPrime(o) self.z2_error = np.matmul(self.o_delta, np.matrix.transpose(self.W2)) self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2) self.W1 += np.matmul(np.matrix.transpose(X), self.z2_delta) self.W2 += np.matmul(np.matrix.transpose(self.z2), self.o_delta)

在上面的代碼片段中，輸出層的輸出錯誤被計算為預(yù)測輸出與實際輸出之間的差值。然后，在重復(fù)整個過程直到到達輸入層之前，將這個錯誤與 Sigmoid 相乘以運行梯度下降法。最后，更新不同層之間的權(quán)重。

步驟4.4: 創(chuàng)建一個訓(xùn)練函數(shù)

在訓(xùn)練過程中，該算法將運行向前和向后傳遞，從而更新每個 epoch 的權(quán)重。為了得到最精確的權(quán)重值，這是必要的。

def train(self, X, y, epochs): for epoch in range(epochs): o = self.forward(X) self.backward(X, y, o) self.error_list.append(np.abs(self.o_error).mean())

除了向前和向后傳播之外，我們還將平均絕對誤差(MAE)保存到一個錯誤列表中，以便日后觀察平均絕對誤差在訓(xùn)練過程中是如何演變的。

步驟4.5: 創(chuàng)建一個預(yù)測函數(shù)

在訓(xùn)練過程中對權(quán)重進行了微調(diào)之后，該算法就可以預(yù)測新數(shù)據(jù)點的輸出。預(yù)測的輸出數(shù)字有望與實際輸出數(shù)字非常接近。

def predict(self, x_predicted): return self.forward(x_predicted).item()

步驟4.6: 繪制平均絕對誤差發(fā)展圖

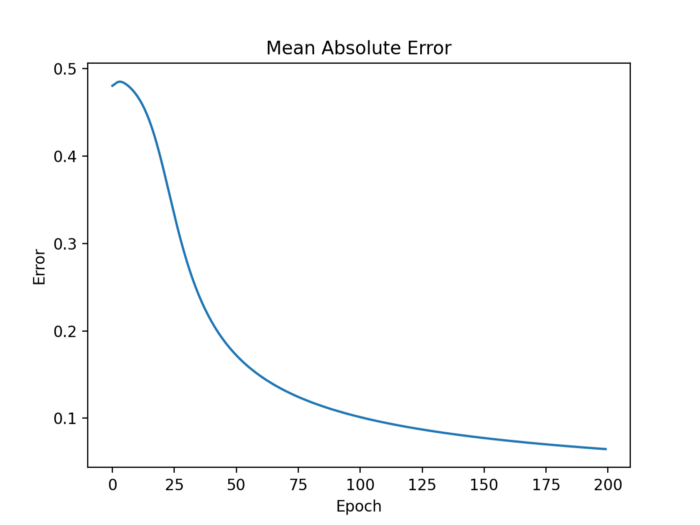
評價機器學(xué)習(xí)算法質(zhì)量的方法有很多。經(jīng)常使用的測量方法之一是平均絕對誤差，這個誤差應(yīng)該隨著時間的推移而減小。

def view_error_development(self): plt.plot(range(len(self.error_list)), self.error_list) plt.title(’Mean Sum Squared Loss’) plt.xlabel(’Epoch’) plt.ylabel(’Loss’)

步驟4.7: 計算精度及其組成部分

真正、假正、真負和假負的數(shù)量描述了機器學(xué)習(xí)分類算法的質(zhì)量。訓(xùn)練后的神經(jīng)網(wǎng)絡(luò)權(quán)值更新，使算法能夠準(zhǔn)確地預(yù)測新的數(shù)據(jù)點。在二進制分類任務(wù)中，這些新數(shù)據(jù)點只能是1或0。根據(jù)預(yù)測值是否高于或低于定義的限制，算法將新條目分為1或0。

def test_evaluation(self, input_test, output_test): for i, test_element in enumerate(input_test): if self.predict(test_element) > self.limit and output_test[i] == 1: self.true_positives += 1 if self.predict(test_element) < self.limit and output_test[i] == 1: self.false_negatives += 1 if self.predict(test_element) > self.limit and output_test[i] == 0: self.false_positives += 1 if self.predict(test_element) < self.limit and output_test[i] == 0: self.true_negatives += 1 print(’True positives: ’, self.true_positives, ’nTrue negatives: ’, self.true_negatives, ’nFalse positives: ’, self.false_positives, ’nFalse negatives: ’, self.false_negatives, ’nAccuracy: ’, (self.true_positives + self.true_negatives) / (self.true_positives + self.true_negatives + self.false_positives + self.false_negatives))

當(dāng)運行 test _ evaluation 函數(shù)時，我們得到以下結(jié)果:

真正: 2

真負: 4

假正: 0

假負: 0

準(zhǔn)確性由以下公式給出：

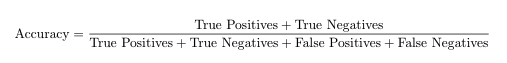
由此我們可以推斷，在我們的案例中，精確度是1。

第五步: 運行一個腳本來訓(xùn)練和評估神經(jīng)網(wǎng)絡(luò)模型

NN = NeuralNetwork()NN.train(input_train_scaled, output_train_scaled, 200)NN.predict(input_pred)NN.view_error_development()NN.test_evaluation(input_test_scaled, output_test_scaled)

為了嘗試我們剛剛構(gòu)建的神經(jīng)網(wǎng)絡(luò)類，我們將首先初始化一個神經(jīng)網(wǎng)絡(luò)類型的對象。然后對訓(xùn)練數(shù)據(jù)進行神經(jīng)網(wǎng)絡(luò)訓(xùn)練，在新訓(xùn)練的模型在測試向量上進行測試之前，對算法的權(quán)值進行200個 epoch 以上的“修正”。然后，在利用測試數(shù)據(jù)集對模型進行評估之前，繪制誤差圖。

第六步: 改進腳本并使用它

提供的代碼可以很容易地修改，以處理其他類似的情況。我們鼓勵讀者嘗試改變變量并使用自己的數(shù)據(jù)等等。改進或變更的潛在想法包括但不限于：

泛化代碼以適用于任何輸入和輸出大小的數(shù)據(jù) 使用平均絕對誤差以外的另一個度量來衡量誤差 使用其他的縮放函數(shù)

到此這篇關(guān)于Python創(chuàng)建簡單的神經(jīng)網(wǎng)絡(luò)實例講解的文章就介紹到這了,更多相關(guān)如何在Python中創(chuàng)建一個簡單的神經(jīng)網(wǎng)絡(luò)內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！